Bei der Konstruktion von Flachfedern, Formfedern und Flachformfedern wird neben der Biegespannung auch häufig das Flächenträgheitsmoment berechnet. Das Flächenträgheitsmoment ist eine geometrische Größe, die in der Festigkeitslehre verwendet wird. Sie wird zur Verformungs- und Spannungsberechnung bei Biege- und Torsionsbeanspruchung von Federn und Metallformteilen herangezogen. Hergeleitet wird das Flächenträgheitsmoment aus dem Querschnitt der Metallformteile. Das Flächenträgheitsmoment wird in mm4 angegeben. Abhängig von der Belastung können zwei unterschiedliche Arten des Flächenträgheitsmoments unterschieden werden.
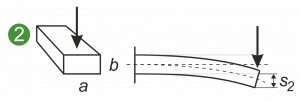
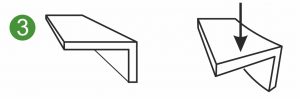
In den folgenden Grafiken sind der symmetrische und asymmetrische Querschnitte einer Flachfeder, Formfedern oder Flachformfeder dargestellt, die unterschiedlichen Belastungen ausgesetzt sind. Die Illustrationen zeigt eine einseitig eingespannte Flachfeder (1 und 2) sowie die Belastung einer Formfedern oder Metallformteils auf Biegung (3).
Inhaltsverzeichnis
Axiales Flächenträgheitsmoment
Das axiale Flächenträgheitsmoment Ia beschreibt den Zusammenhang von Flachfederquerschnitt und Krümmung einer Flachfeder unter Belastung. Dabei gilt: Je größer Ia, desto kleiner sind die Krümmung und die im Querschnitt entstehenden inneren Spannungen. Wesentlich ist hier die Ausdehnung in Richtung der angreifenden Kraft. Das Schaubild illustriert, dass eine vertikale Krafteinwirkung eine Flachfeder weniger verbiegt, wenn diese hochkant anstatt flach eingespannt ist (1 und 2). Das axiale
Flächenträgheitsmoment wird mit folgenden Formeln berechnet:
\Large Iy=\int_{} z^{2} dA- z = senkrechter Abstand der y-Achse zum Element dA
- y = senkrechter Abstand der z-Achse zum Element dA
Biaxiales Flächenträgheitsmoment
Das biaxiale Flächenträgheitsmoment Iyz wird auch als Flächendeviationsmoment oder Flächenzentrifugalmoment bezeichnet. Iyz wird zur Berechnung der Verformung und der Spannungen bei belasteten Formfedern, Flachformfedern und asymmetrischen Metallformteilen (3) verwendet.
\Large Iyz=Izy=\int_{} yz dADiese Größe ist auch als Deviations- oder Zentrifugalmoment bekannt. Sie ist gleich Null, wenn die y- oder die z-Achse eine Symmetrieachse des Querschnitts ist.
\Large Iyz = 0
Abgeleitete Größen
Aus dem Flächenträgheitsmoment können verschiedene weitere Größen abgeleitet werden, etwa das Widerstandsmoment und der Flächenträgheitsradius.
Widerstandsmoment
Das Widerstandsmoment findet in der linearen Elastizitätstheorie Anwendung. Damit wird die am Querschnitts-Rand auftretende größte Beanspruchung, die mechanische Spannung, bestimmt. Bei dieser Größe handelt es sich um den Quotienten aus dem Flächenträgheitsmoment und dem Abstand des Rands von der neutralen Faser:
W:=\frac{I}{\alpha max}
Flächenträgheitsradius
Für geometrisch ähnliche Bauteile, etwa Rechtecke mit gleichem Breiten-Höhen-Verhältnis, lässt sich auch der Flächenträgheitsradius mit der Dimension Länge definieren. Damit kann man Körper vergleichen, die in Durchbiegung und Steifigkeit ähnlich sind. Der Flächenträgheitsradius ist im Schlankheitsgrad enthalten.
\Large iy:=\sqrt{\frac{Iy}{A}} \Large iz:=\sqrt{\frac{Iz}{A}} \Large ip:=\sqrt{\frac{Ip}{A}}
Sehen Sie hier weitere Informationen zur Berechnung von Flachfedern, Formfedern und Flachformfedern. Wenn Sie für Ihre spezielle Anwendung eine technische Feder suchen, dann senden Sie uns einfach unter nachfolgendem Anfragebutton „Federnanfrage“ oder per E-Mail info@gutekunst-formfedern.de die gewünschten Federdaten mit Angabe der benötigten Stückzahl und der Zeichnung oder den CAD-Daten zu. Wir erstellen Ihnen kurzfristig ein unverbindliches Angebot.
Weitere Informationen: