In the design of flat springs, shaped springs and flat shaped springs, the area moment of inertia is often calculated in addition to the bending stress. The area moment of inertia is a geometric quantity used in strength theory. It is used for deformation and stress calculation in bending and torsion loading of springs and metal formed parts. The area moment of inertia is derived from the cross-section of the shaped metal parts. The area moment of inertia is specified in mm4. Depending on the load, two different types of area moment of inertia can be distinguished.
The following diagrams show the symmetrical and asymmetrical cross-sections of a flat spring, shaped spring or flat shaped spring subjected to different loads. The illustrations show a flat spring clamped on one side(1 and 2) and the loading of a shaped spring or metal part in bending(3).
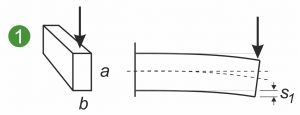
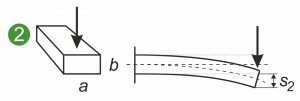
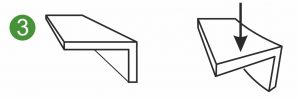
Table of Contents
Axial surface moment of inertia
The axial area moment of inertia Ia describes the relationship between the flat spring cross-section and the curvature of a flat spring under load. The following applies: The larger Ia, the smaller the curvature and the internal stresses arising in the cross-section. What is essential here is the expansion in the direction of the attacking force. The diagram illustrates that a vertical force bends a flat spring less when it is clamped on edge instead of flat(1 and 2). The axial
Area moment of inertia is calculated with the following formulas:
\Large Iy=\int_{} z^{2} dA- z = perpendicular distance of the y-axis to the element dA
- y = perpendicular distance of the z-axis to the element dA
biaxial surface moment of inertia
The biaxial surface moment of inertia Iyz is also called surface moment of deviation or surface centrifugal moment. Iyz is used to calculate the deformation and stresses in loaded shaped springs, flat shaped springs and asymmetrical metal shaped parts(3).
\Large Iyz=Izy=\int_{} yz dAThis quantity is also known as the deviation or centrifugal moment. It is equal to zero if the y-axis or the z-axis is an axis of symmetry of the cross section.
\Large Iyz = 0
Derived quantities
Various other quantities can be derived from the surface moment of inertia, such as the section modulus and the surface radius of inertia.
Resistance torque
The section modulus is used in linear elasticity theory. This determines the greatest stress occurring at the edge of the cross-section, the mechanical stress. This value is the quotient of the area moment of inertia and the distance of the edge from the neutral fiber:
\Large W:=\frac{I}{\alpha max}
Area radius of gyration
For geometrically similar components, such as rectangles with the same width-height ratio, the surface radius of inertia can also be defined with the dimension length. This allows you to compare bodies that are similar in deflection and stiffness. The surface radius of inertia is included in the slenderness ratio.
\Large iy:=\sqrt{\frac{Iy}{A}} \Large iz:=\sqrt{\frac{Iz}{A}} \Large ip:=\sqrt{\frac{Ip}{A}}
See here for more information on the calculation of flat springs, shaped springs and flat shaped springs. If you are looking for a technical spring for your special application, then simply send us the required spring data with details of the required quantity and the drawing or CAD data under the following enquiry button “Spring enquiry” or by email info@gutekunst-formfedern.de. We will prepare a non-binding offer for you at short notice.
For more information: