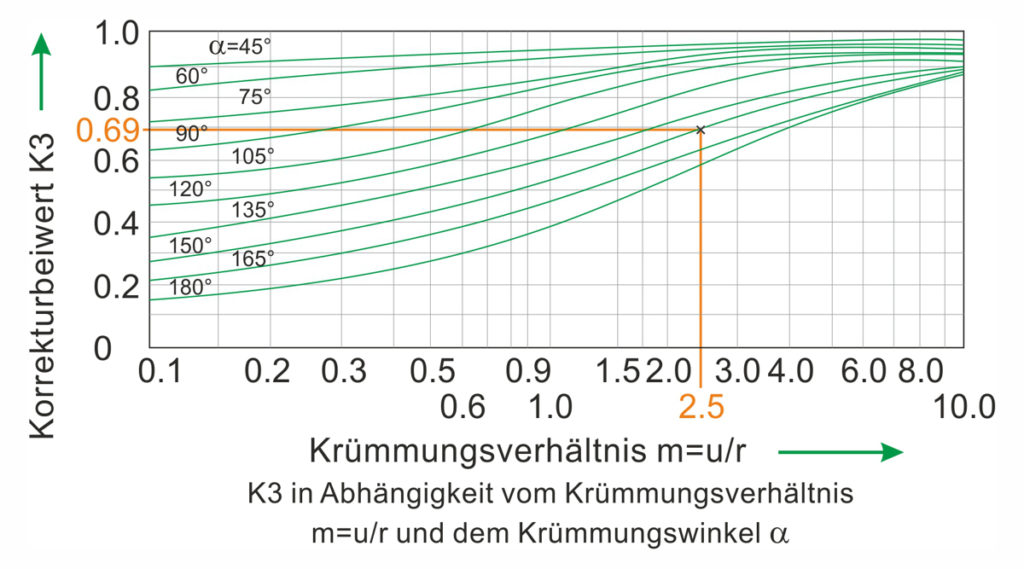
Für die Berechnung einer einfachen Flachformfeder, bzw. gekrümmten Blattfeder oder Formfeder, mit Rechteckquerschnitt können folgende Formeln für die Verformung “s”, Biegespannung “σb”, Federarbeit “WF” und den Ausnutzwert “ηA” angewendet werden. Bei der Berechnung der Verformung wird die gestreckte Länge (Summe aus geraden und kreisförmigen Federabschnitten) der Flachformfeder und die Steifigkeitsänderung aufgrund der gekrümmten Federform verwendet. Die Steifigkeitsänderung einer Flachformfeder, im Gegensatz zu einer geraden Flachfeder, wird über den Korrekturbeiwert “K3” (siehe nachfolgendes Nomogramm) berücksichtigt. Der Korrekturbeiwert “K3” ist abhängig vom Krümmungsverhältnis “m” (m=u/r), vom geraden Federabschnitts “u” sowie dem Krümmungsradius “r” und Krümmungswinkel “α” des kreisförmigen Federabschnitts. Zur Berechnung der größten Biegespannung “σbmax” ist zu beachten, dass das größte Biegemoment “Mbmax” nicht an der Einspannstelle, sondern am größten Kraftwirkundabstand auftritt.
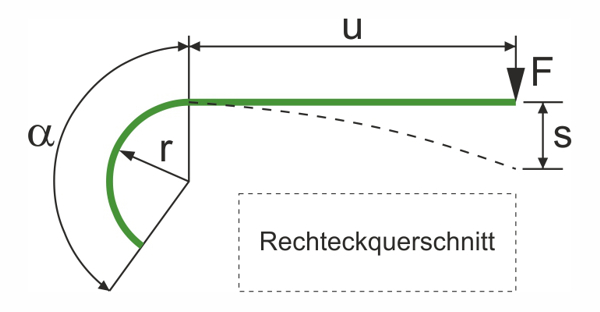
- α: Krümmungswinkel (°)
- b: Breite der Flachformfeder (mm)
- E: Elastizitätsmodul
- h: Stärke der Flachformfeder (mm)
- K3: Korrekturbeiwert (siehe nachfolgendes Nomogramm)
- Iz: Flächenträgheitsmoment (Z-Achse)
- l: Gestreckte Länge der Feder (mm)
- m=u/r: Krümmungsverhältnis
- r: Krümmungsradius (°)
- u: Länge des geraden Federabschnitts (mm)
- Wb: Widerstandsmoment
Formeln:
Table of Contents
1. Flächenträgheitsmoment
\Large Iz = \frac{bh^{3}}{12}
2. Verformung
\Large s = K3 \cdot \frac{F \cdot l^{3}}{3 \cdot E \cdot Iz}
oder
\Large s = K3 \cdot \frac{F}{3 \cdot E \cdot Iz} (u + r\alpha)^{3}
3. Biegespannung
\Large Mbmax = F \cdot (u + r)
\Large \sigma bmax = \frac{Mbmax}{Wb}\leq \sigma bzul
\Large Wb = \frac{bh^{2}}{6}
4. Federarbeit
\Large WF = \frac{1}{2} \cdot Fs = \frac{1}{2} \cdot K3 \cdot \frac{F^{2}}{3EI} \cdot (u + ra)^{3}
5. Ausnutzwert
\Large \eta A = \frac{1}{9} \cdot K3 \cdot \frac{(u + r\alpha)^{2}}{(u + r)^{2}}
Nomogramm Korrekturbeiwert K3
Gutekunst Formfedern entwickelt und fertigt individuelle Flachformfedern und Formfedern als Muster oder Prototypen sowie in Kleinmengen und Großserien. Senden Sie uns einfach unter nachfolgendem Anfragebutton „Federnanfrage“ oder per E-Mail info@gutekunst-formfedern.de die Daten ihrer gewünschten Flachformfeder und Formfeder mit Angabe der Stückzahl und der Zeichnung oder den CAD-Daten. Wir erstellen Ihnen kurzfristig ein unverbindliches Angebot.
Profitieren Sie vom neuen Formfedern-Shop
Der neue Formfedern-Shop von Gutekunst Formfedern bietet mehrere Vorteile in der Beschaffung von Formfedern, Flachfedern, Laserteilen und Blechteilen. Durch die einfache Bedienung, die transparente Online-Preiskalkulation und die schnelle digitale Abwicklung ist er für Konstrukteure, Techniker und Einkäufer eine echte Unterstützung. Endlich lassen sich maßgeschneiderte Metallformteile unkompliziert und zeitsparend konfigurieren, Preise kalkulieren, anfragen und bestellen – rund um die Uhr und mit maximaler Transparenz.
Probieren Sie es am besten gleich selbst aus unter https://shop.formfedern.com
Formfedern-Shop
Weitere Informationen