Obliczyć moment bezwładności powierzchni › Gutekunst Formfedern GmbH

Przy projektowaniu sprężyn płaskich, sprężyn kształtowych i sprężyn płasko profilowanych często oprócz naprężeń zginających oblicza się również moment bezwładności powierzchni. Moment bezwładności powierzchni jest wielkością geometryczną stosowaną w teorii wytrzymałości. Służy do obliczania odkształceń i naprężeń przy zginaniu i skręcaniu sprężyn i kształtek metalowych. Obszarowy moment bezwładności wynika z przekroju poprzecznego listew metalowych. Moment bezwładności powierzchni podany jest w mm4. W zależności od obciążenia można wyróżnić dwa różne rodzaje powierzchniowego momentu bezwładności.

Poniższe wykresy przedstawiają symetryczne i niesymetryczne przekroje poprzeczne sprężyny płaskiej, sprężyny kształtowej lub sprężyny płasko-kształtnej poddanej różnym obciążeniom. Ilustracje pokazują sprężynę płaską zaciśniętą z jednej strony(1 i 2) oraz obciążenie sprężyny kształtowej lub listwy metalowej przy zginaniu(3).

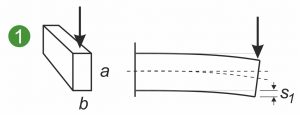
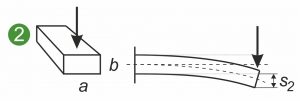
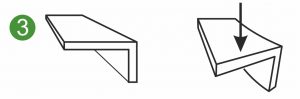
Table of Contents

Moment bezwładności powierzchni osiowej

Osiowy powierzchniowy moment bezwładności Ia opisuje zależność pomiędzy przekrojem poprzecznym sprężyny płaskiej a krzywizną sprężyny płaskiej pod obciążeniem. Obowiązuje następująca zasada: im większe Ia, tym mniejsza krzywizna i naprężenia wewnętrzne powstające w przekroju poprzecznym. Istotna jest tu ekspansja w kierunku siły atakującej. Na rysunku pokazano, że siła pionowa mniej ugina sprężynę płaską, gdy jest ona zaciśnięta na krawędzi, a nie na płasko(1 i 2). Osiowy

Moment bezwładności powierzchni obliczany jest według następujących wzorów:

$Iy=int_{} z^{2} dA$

z = odległość prostopadła osi y do elementu dA

$Iz=int_{} y^{2} dA$

y = odległość prostopadła osi z do elementu dA

Dwuosiowy moment bezwładności powierzchni

Dwuosiowy powierzchniowy moment bezwładności Iyz nazywany jest również powierzchniowym momentem dewiacyjnym lub powierzchniowym momentem odśrodkowym. Iyz jest stosowany do obliczania odkształceń i naprężeń w obciążonych sprężynach kształtowych, płaskich sprężynach kształtowych i asymetrycznych metalowych częściach kształtowych(3).

$Iyz=Izy=int_{} yz dA$

Wielkość ta znana jest również jako odchylenie lub moment odśrodkowy. Jest on równy zeru, jeżeli oś y lub oś z jest osią symetrii przekroju poprzecznego.

Iyz = 0

Ilości pochodne

Z momentu bezwładności można wyprowadzić różne inne wielkości, takie jak moment oporu i promień bezwładności powierzchni.

Moment oporu

Moduł przekroju jest stosowany w teorii sprężystości liniowej. Określa to największe naprężenie występujące na krawędzi przekroju poprzecznego, naprężenie mechaniczne. Wartość ta jest ilorazem momentu bezwładności powierzchni i odległości $\alpha _m_a_x}$ krawędzi od włókna neutralnego:

$W:=frac{I}{{alpha _m_a_x}$

Promień bezwładności powierzchni

Dla geometrycznie podobnych elementów, takich jak prostokąty o tym samym stosunku szerokości do wysokości, promień bezwładności powierzchni może być również określony za pomocą długości. Pozwala to na porównanie ciał, które są podobne pod względem ugięcia i sztywności. Promień bezwładności powierzchni jest zawarty we współczynniku smukłości.

$iy:=sqrt{frac{Iy}{A}}$

$iz:=sqrt{frac{Iz}{A}}$

$ip:=sqrt{frac{Ip}{A}}$

Więcej informacji na temat obliczania sprężyn płaskich, sprężyn kształtowych i sprężyn płaskich można znaleźć tutaj. Jeżeli poszukujecie Państwo sprężyny technicznej do specjalnego zastosowania, to prosimy o przesłanie nam danych dotyczących sprężyny z podaniem ilości sztuk oraz rysunków lub danych CAD za pomocą przycisku”Zapytanie o sprężynę” lub e-mailem info@gutekunst-formfedern.de. W krótkim czasie przedstawimy Ci niewiążącą ofertę.

Federnanfrage

Dodatkowe informacje: