Calcular o momento de inércia da área › Gutekunst Formfedern GmbH › Cálculo da deformação, Cálculo do stress, Carga, Molas, Molas de forma, Molas em forma plana, Molas planas, Momento de inércia da área, Tensão de flexão, Tensão de torção, Torque de Resistência

Na concepção de molas planas, molas de forma e molas de forma plana, o momento de inércia da área é muitas vezes calculado para além da tensão de flexão. O momento de inércia da área é uma quantidade geométrica utilizada na teoria da força. É utilizado para o cálculo de deformações e tensões na flexão e tensão de torção de molas e moldes metálicos. O momento de inércia da área é derivado da secção transversal das molduras metálicas. O momento de inércia da área é dado em mm4. Dependendo da carga, é possível distinguir dois tipos diferentes de momento de inércia de área.

Os gráficos seguintes mostram as secções transversais simétricas e assimétricas de uma mola plana, mola de forma ou mola de forma plana sujeita a diferentes cargas. As ilustrações mostram uma mola plana fixada de um lado(1 e 2) e o carregamento de uma mola moldada ou moldagem metálica na dobra(3).

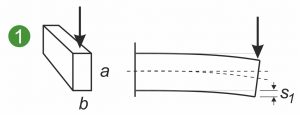
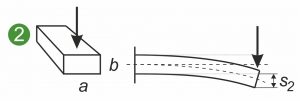
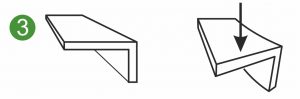
Table of Contents

Momento de inércia da superfície axial

O momento axial de inércia Ia da superfície descreve a relação entre a seção transversal da mola plana e a curvatura de uma mola plana sob carga. Aplica-se o seguinte: Quanto maior a Ia, menor a curvatura e as tensões internas que surgem na secção transversal. O que é essencial aqui é a expansão na direção da força atacante. O diagrama ilustra que uma força vertical dobra menos uma mola plana quando está presa à borda em vez de plana(1 e 2). O axial

O momento de inércia da área é calculado com as seguintes fórmulas:

$Iy=\int_{} z^{2} dA$

z = distância perpendicular do eixo y ao elemento dA

$Iz=\int_{} y^{2} dA$

y = distância perpendicular do eixo z ao elemento dA

Momento de inércia da superfície biaxial

O momento superficial biaxial de inércia Iyz também é chamado de momento de desvio superficial ou momento centrífugo superficial. A Iyz é utilizada para calcular a deformação e as tensões em molas em forma de carga, molas em forma plana e peças assimétricas em forma de metal(3).

$Iyz=Izy=\int_{} yz dA$

Esta quantidade também é conhecida como o desvio ou momento centrífugo. É igual a zero se o eixo y ou o eixo z for um eixo de simetria da secção transversal.

Iyz = 0

Quantidades derivadas

Várias outras quantidades podem ser derivadas do momento de inércia, tais como o momento de resistência e o raio de superfície de inércia.

Torque de Resistência

O módulo de seção é usado na teoria da elasticidade linear. Isto determina a maior tensão que ocorre na extremidade da secção transversal, a tensão mecânica. Este valor é o quociente entre o momento de inércia da área e a distância $\alpha _m_a_x}$ da borda em relação à fibra neutra:

$W:=frac{I}{\i1}alpha _m_a_x}$

Raio de inércia da área

Para componentes geometricamente semelhantes, tais como rectângulos com a mesma relação largura-altura, o raio de inércia da área também pode ser definido com o comprimento da dimensão. Isto permite comparar corpos que são semelhantes em deflexão e rigidez. O raio de inércia da área está incluído na razão de esguelha.

$iy:=sqrt{\frac{Iy}{A}}$

$iz:=sqrt{\frac{Iz}{A}}$

$ip:=sqrt{\frac{Ip}{A}}$

Veja aqui para mais informações sobre o cálculo de molas planas, molas de forma e molas de forma plana. Se você está procurando uma mola técnica para a sua aplicação especial, basta enviar-nos os dados necessários da mola com detalhes do número de peças necessárias e os dados do desenho ou CAD usando o seguinte botão de consulta”Consulta da mola” ou pelo e-mail info@gutekunst-formfedern.de. Faremos uma oferta não vinculativa em cima da hora.

Federnanfrage

Para mais informações: