 Lors de la conception de ressorts plats, de ressorts de forme et de ressorts de forme plats, on calcule souvent, en plus de la contrainte de flexion, le moment d’inertie de la surface. Le moment d’inertie de surface est une grandeur géométrique utilisée dans la théorie de la résistance. Elle est utilisée pour calculer les déformations et les contraintes en cas de flexion et de torsion des ressorts et des pièces métalliques moulées. Le moment d’inertie de surface est déduit de la section transversale des pièces métalliques moulées. Le moment d’inertie de la surface est exprimé en mm4. En fonction de la charge, on peut distinguer deux types différents de moment d’inertie de surface.
Lors de la conception de ressorts plats, de ressorts de forme et de ressorts de forme plats, on calcule souvent, en plus de la contrainte de flexion, le moment d’inertie de la surface. Le moment d’inertie de surface est une grandeur géométrique utilisée dans la théorie de la résistance. Elle est utilisée pour calculer les déformations et les contraintes en cas de flexion et de torsion des ressorts et des pièces métalliques moulées. Le moment d’inertie de surface est déduit de la section transversale des pièces métalliques moulées. Le moment d’inertie de la surface est exprimé en mm4. En fonction de la charge, on peut distinguer deux types différents de moment d’inertie de surface.
Les graphiques suivants représentent les sections symétriques et asymétriques d’un ressort plat, d’un ressort de forme ou d’un ressort de forme plat soumis à différentes charges. Les illustrations montrent un ressort plat encastré d’un côté(1 et 2) ainsi que la sollicitation en flexion d’un ressort de forme ou d’une pièce métallique moulée(3).
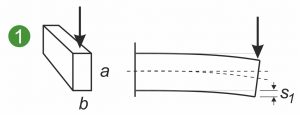
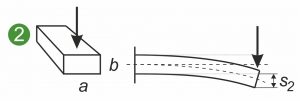
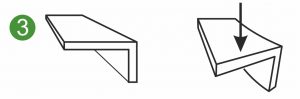
Table of Contents
Moment d’inertie axial de la surface
Le moment d’inertie axial de surface Ia décrit la relation entre la section transversale du ressort plat et la courbure d’un ressort plat sous charge. La règle est la suivante : plus Ia est grand, plus la courbure et les tensions internes générées dans la section sont faibles. L’essentiel est ici la dilatation dans la direction de la force d’attaque. Le graphique illustre le fait qu’une force verticale déforme moins un ressort plat lorsque celui-ci est serré de chant plutôt qu’à plat(1 et 2). Le système axial
Le moment d’inertie de la surface est calculé à l’aide des formules suivantes :
\Large Iy=\int_{} z^{2} dA- z = distance perpendiculaire de l’axe y à l’élément dA
- y = distance perpendiculaire de l’axe z à l’élément dA
Moment d’inertie de surface biaxial
Le moment d’inertie biaxial de surface Iyz est également appelé moment de déformation de surface ou moment centrifuge de surface. Iyz est utilisé pour calculer la déformation et les contraintes des ressorts de forme chargés, des ressorts de forme plats et des pièces métalliques moulées asymétriques(3).
\Large Iyz=Izy=\int_{} yz dACette grandeur est également connue sous le nom de moment de déviation ou de moment centrifuge. Elle est égale à zéro si l’axe y ou l’axe z est un axe de symétrie de la section.
\Large Iyz = 0
Grandeurs dérivées
Plusieurs autres grandeurs peuvent être déduites du moment d’inertie de la surface, comme le moment de résistance et le rayon d’inertie de la surface.
Couple de résistance
Le moment de résistance est utilisé dans la théorie de l’élasticité linéaire. On détermine ainsi la contrainte la plus importante apparaissant au bord de la section, la contrainte mécanique. Il s’agit du quotient du moment d’inertie de la surface par la distance entre le bord et la fibre neutre :
\Large W:=\frac{I}{\alpha max}
Rayon d’inertie de la surface
Pour les éléments de construction géométriquement similaires, tels que les rectangles ayant le même rapport largeur/hauteur, il est également possible de définir le rayon d’inertie de la surface avec la dimension longueur. On peut ainsi comparer des corps dont la flexion et la rigidité sont similaires. Le rayon d’inertie de la surface est inclus dans l’élancement.
\Large iy:=\sqrt{frac{Iy}{A}} \Large iz:=\sqrt{frac{Iz}{A}} \Large ip:=\sqrt{frac{Ip}{A}}
Consultez ici plus d’informations sur le calcul des ressorts plats, des ressorts de forme et des ressorts de forme plats. Si vous recherchez un ressort technique pour votre application spécifique, il vous suffit de nous envoyer les données du ressort souhaité en cliquant sur le bouton de demande suivant « Demande de ressort » ou par e-mail info@gutekunst-formfedern.de en indiquant la quantité nécessaire et le dessin ou les données CAO. Nous vous ferons une offre sans engagement dans un bref délai.
Information additionnelle:
