Vypočítejte geometrický moment setrvačnosti

Při navrhování plochých pružin , tvarových pružin a plochých tvarových pružin se kromě namáhání v ohybu často počítá také s geometrickým momentem setrvačnosti. Geometrický moment setrvačnosti je geometrická veličina, která se používá v pevnostním inženýrství. Používá se k výpočtu deformace a napětí v případě ohybového a torzního zatížení pružin a kovových lisovaných dílů. Geometrický moment setrvačnosti je odvozen z průřezu lisovaných kovových dílů. Geometrický moment setrvačnosti se udává v mm ⁴ . V závislosti na zatížení lze rozlišit dva různé typy geometrického momentu setrvačnosti.

Následující grafika ukazuje symetrické a nesymetrické průřezy ploché pružiny, tvarové pružiny nebo ploché pružiny, které jsou vystaveny různému zatížení. Na obrázku je na jedné straně upnutá plochá pružina ( 1 a 2 ) a také zatížení tvarové pružiny nebo tvarového kovového dílu při ohybu ( 3 ).

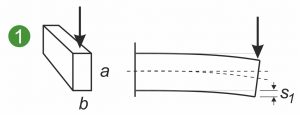
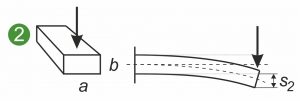
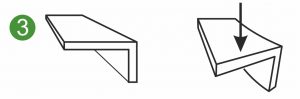
Table of Contents

Axiální druhý moment plochy

Axiální geometrický moment setrvačnosti Ia popisuje vztah mezi plochým průřezem pružiny a zakřivením ploché pružiny při zatížení. Platí: čím větší Ia , tím menší zakřivení a vnitřní napětí , která v průřezu vznikají. Podstatné je zde rozšíření ve směru útočící síly. Diagram ukazuje, že svislá síla ohýbá plochou pružinu méně, pokud je upnutá svisle místo naplocho ( 1 a 2 ). Axiální

Plošný moment setrvačnosti se vypočítá pomocí následujících vzorců:

$Iy = \ int_ {} z ^{2} tam$

z = vertikální vzdálenost osy y k prvku dA

$Iz = \ int_ {} y ^{2} tam$

y = vertikální vzdálenost osy z k prvku dA

Dvojosý moment plochy

Dvojosý plošný moment setrvačnosti Iyz je také označován jako plošný odchylkový moment nebo plošný odstředivý moment. Iyz se používá k výpočtu deformace a napětí v zatížených tvarových pružinách, plochých pružinách a asymetricky tvarovaných kovových dílech ( 3 ).

$Iyz = Izy = \ int_ {} yz dA$

Tato veličina je také známá jako odchylka nebo odstředivý moment. Je roven nule, pokud je osa y nebo osa z osou symetrie průřezu.

Iyz = 0

Odvozená množství

Z plošného momentu setrvačnosti lze odvodit různé další proměnné, jako je moment odporu a plošný poloměr setrvačnosti.

Okamžik odporu

Modul průřezu se používá v lineární teorii pružnosti. To určuje největší napětí vyskytující se na okraji průřezu, mechanické napětí. Tato proměnná je podílem plošného momentu setrvačnosti a vzdálenosti $\ alfa _m_a_x}$ okraje neutrálního vlákna:

$W: = \ frac{I} {\ alpha _m_a_x}$

Plošný poloměr setrvačnosti

Pro geometricky podobné součásti, jako jsou obdélníky se stejným poměrem šířky k výšce, lze oblastní poloměr otáčení definovat také pomocí délky kóty. To vám umožní porovnat tělesa, která jsou podobná z hlediska průhybu a tuhosti. Plošný poloměr otáčení je zahrnut v poměru štíhlosti.

$iy: = \ sqrt {\ frac{Iy}{A} }$

$iz: = \ sqrt {\ frac{Iz}{A} }$

$ip: = \ sqrt {\ frac{Ip}{A} }$

Zde můžete vidět další informace o výpočtu plochých pružin , tvarových pružin a plochých tvarových pružin. Pokud hledáte technickou pružinu pro vaši speciální aplikaci, pak nám jednoduše zašlete požadovaná data pružiny s požadovaným počtem kusů a výkresem nebo CAD daty pod následujícím poptávkovým tlačítkem “ Jarní poptávka “ nebo e-mailem na info@gutekunst-formfedern.de to. V krátké době vám dáme nezávaznou nabídku.

Federnanfrage

Dodatečné informace: