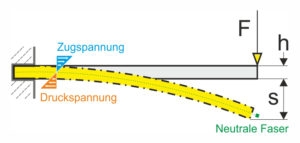
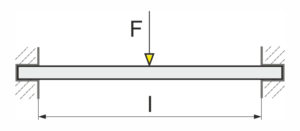
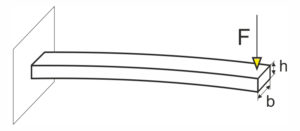
Die Biegespannung, die bei der Biegung einer Flachfeder, Blattfeder oder Flachformfeder auftritt, lässt sich am Beispiel der einseitig eingespannten Flachfeder verdeutlichen: Die Flachfeder mit der ursprünglichen Länge „l“ wird bei der Verbiegung durch die Kraft „F“ auf der Oberseite verlängert und auf der Unterseite gestaucht. Daraus resultierend wirken an der Oberseite Zugspannungen und an der Unterseite Druckspannungen. In der Mitte des Balkens befindet sich ein Übergangsbereich, die spannungsfreie Zone, welche ihre Länge bei der Biegung nicht ändert. Betrachtet man das Innere der Flachfeder, ist die Biegespannung „“ in der Randfaser mit dem größten Abstand zur neutralen Faser am höchsten. Somit wächst die Biegespannung proportional zum Abstand der neutralen Faser an (Hookesches Gesetz). Die neutrale Faser geht durch den Massenschwerpunkte der Flachfederquerschnitts.
Table of Contents
Formel Biegespannung
Für die Berechnung der Biegespannung „\Large \sigma_{{b}}“ [Nmm²] wird folgendes benötigt: das Biegemoment „Mb“ [Nmm] und das Widerstandsmoment „W“ [mm³].
\Large\sigma_{b} = \frac{Mb}{W}
Berechnung des Biegemoment „Mb“
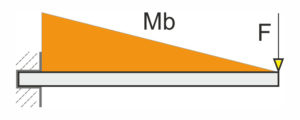
Das Biegemoment „Mb“ ist von der Art der Krafteinwirkung auf die Flachfeder oder Blattfeder und der Lagerung der Enden abhängig. Für die Berechnung des Biegemoment stehen folgende Berechnungsvarianten zur Verfügung, die jeweils das maximale Biegemoment berechnen:
Das Biegemoment an der Flachfeder ist an der Einleitungsstelle der Kraft gleich Null. Bis zur Einspannstelle steigt es linear auf seinen maximalen Wert an. Querschnitt und Materialeigenschaften sind entlang der Flachfeder konstant.
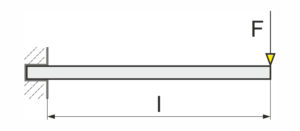
- maximale Biegemoment [Nmm] bei einseitig eingespannter Flachfeder
\Large Mb = F \cdot l
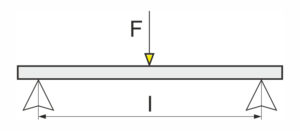
- maximale Biegemoment [Nmm] berechnen bei beidseitig gestützter Flachfeder
\Large Mb = \frac{F \cdot l}{4}
- maximale Biegemoment [Nmm] berechnen bei beidseitig eingespannter Flachfeder
\Large Mb = \frac{F \cdot l}{8}
Berechnung Widerstandsmoment „W“
Das Widerstandsmoment „W“ [mm³] berücksichtigt den Widerstand gegen die Durchbiegung. Aus diesem Grund wird es häufig als Biegewiderstandsmoment bezeichnet. Für die Größe „Widerstandsmoment“ ist allein die Geometrie (Breite x Höhe in mm) der jeweils betrachteten Formfeder-Querschnittsfläche ausschlaggebend.
\Large W = \frac{I}{\alpha_{max}}
\Large I = \frac{bh^{3}}{12}
\Large \alpha_{{max}} = \frac{h}{2}
W = Widerstandsmoment
\Large \alpha_{{max}} = Abstand der Randfaser zur neutralen Faser
Hier finden Sie mehr Informationen zur Berechnung von Flachfedern, Blattfedern und Flachformfedern. Und wenn Sie wissen möchten welche technische Feder für Ihre spezielle Anwendung am besten geeignet ist? Dann senden Sie uns einfach unter nachfolgendem Anfrageformular oder per E-Mail info@gutekunst-formfedern.de die Daten der gewünschten Flachfeder, Flachformfeder und Formfeder mit Angabe der Stückzahl und der Zeichnung, Skizze oder den CAD-Daten. Wir erstellen Ihnen kurzfristig ein unverbindliches Angebot.
Anfrage Formfedern & Blattfedern
Weitere Informationen: