 Nella progettazione di molle piatte, molle sagomate e molle piatte sagomate, il momento d’inerzia dell’area è spesso calcolato in aggiunta alla sollecitazione di flessione. Il momento d’inerzia dell’area è una grandezza geometrica usata nella teoria della resistenza. Viene utilizzato per il calcolo delle deformazioni e delle sollecitazioni in flessione e torsione di molle e stampi metallici. Il momento d’inerzia dell’area è derivato dalla sezione trasversale degli stampi metallici. Il momento d’inerzia dell’area è specificato in mm4. A seconda del carico, si possono distinguere due diversi tipi di momento d’inerzia d’area.
Nella progettazione di molle piatte, molle sagomate e molle piatte sagomate, il momento d’inerzia dell’area è spesso calcolato in aggiunta alla sollecitazione di flessione. Il momento d’inerzia dell’area è una grandezza geometrica usata nella teoria della resistenza. Viene utilizzato per il calcolo delle deformazioni e delle sollecitazioni in flessione e torsione di molle e stampi metallici. Il momento d’inerzia dell’area è derivato dalla sezione trasversale degli stampi metallici. Il momento d’inerzia dell’area è specificato in mm4. A seconda del carico, si possono distinguere due diversi tipi di momento d’inerzia d’area.
I seguenti grafici mostrano le sezioni simmetriche e asimmetriche di una molla piatta, una molla sagomata o una molla piatta sagomata sottoposta a diversi carichi. Le illustrazioni mostrano una molla piatta bloccata su un lato(1 e 2) e il caricamento di una molla sagomata o di uno stampo metallico in flessione(3).
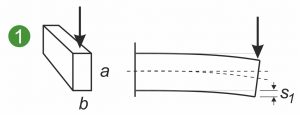
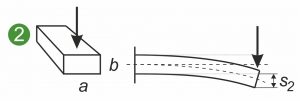
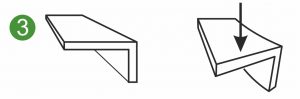
Table of Contents
Momento d’inerzia della superficie assiale
Il momento d’inerzia superficiale assiale Ia descrive la relazione tra la sezione trasversale della molla piatta e la curvatura di una molla piatta sotto carico. Vale quanto segue: più grande è Ia, più piccola è la curvatura e le tensioni interne che sorgono nella sezione trasversale. Ciò che è essenziale qui è l’espansione nella direzione della forza attaccante. Il diagramma illustra che una forza verticale piega meno una molla piatta quando è bloccata sul bordo invece che piatta(1 e 2). L’assiale
Il momento d’inerzia dell’area è calcolato con le seguenti formule:
\Large Iy=\int_{} z^{2} dA- z = distanza perpendicolare dell’asse y all’elemento dA
- y = distanza perpendicolare dell’asse z all’elemento dA
Momento d’inerzia della superficie biassiale
Il momento d’inerzia superficiale biassiale Iyz è anche chiamato momento di deviazione superficiale o momento centrifugo superficiale. Iyz è usato per calcolare la deformazione e le sollecitazioni in molle sagomate caricate, molle sagomate piatte e parti sagomate asimmetriche in metallo(3).
\Large Iyz=Izy=int_{} yz dAQuesta quantità è anche conosciuta come deviazione o momento centrifugo. È uguale a zero se l’asse y o l’asse z è un asse di simmetria della sezione trasversale.
\Large Iyz = 0
Quantità derivate
Varie altre quantità possono essere derivate dal momento d’inerzia, come il momento di resistenza e il raggio d’inerzia della superficie.
Coppia di resistenza
Il modulo di sezione è usato nella teoria dell’elasticità lineare. Questo determina la massima sollecitazione che si verifica sul bordo della sezione trasversale, la sollecitazione meccanica. Questo valore è il quoziente del momento di inerzia dell’area e della distanza del bordo dalla fibra neutra:
\Large W:=frac{I}{alpha max}
Area raggio d’inerzia
Per componenti geometricamente simili, come rettangoli con lo stesso rapporto larghezza-altezza, il raggio d’inerzia dell’area può anche essere definito con la lunghezza della dimensione. Questo permette di confrontare corpi che sono simili per deflessione e rigidità. Il raggio d’inerzia dell’area è incluso nel rapporto di snellezza.
\Large iy:=\sqrt{\frac{Iy}{A}} \Large iz:=\sqrt{\frac{Iz}{A}} \Large ip:=\sqrt{\frac{Ip}{A}}
Vedi qui per maggiori informazioni sul calcolo delle molle piatte, delle molle sagomate e delle molle piatte sagomate. Se state cercando una molla tecnica per la vostra applicazione speciale, allora inviateci semplicemente i dati della molla richiesta con i dettagli del numero di pezzi richiesti e il disegno o i dati CAD utilizzando il seguente pulsante di richiesta“Richiesta di molla” o via e-mail info@gutekunst-formfedern.de. Ti faremo un’offerta non vincolante con breve preavviso.
Informazioni aggiuntive:
