Számítsa ki a geometriai tehetetlenségi nyomatékot!

Lapos rugók , idomrugók és lapos idomrugók tervezésekor a hajlítófeszültség mellett gyakran számítják a geometriai tehetetlenségi nyomatékot is. A geometriai tehetetlenségi nyomaték egy geometriai mennyiség, amelyet a szilárdságtechnikában használnak. A rugók és fémöntött alkatrészek hajlítási és torziós terhelései esetén a deformáció és feszültség kiszámítására szolgál. A geometriai tehetetlenségi nyomaték az öntött fémrészek keresztmetszetéből adódik. A geometriai tehetetlenségi nyomaték mm ⁴ -ben van megadva. A terheléstől függően két különböző típusú geometriai tehetetlenségi nyomaték különböztethető meg.

A következő grafikonok egy lapos rugó, alakrugó vagy laprugó szimmetrikus és aszimmetrikus keresztmetszeteit mutatják be , amelyek különböző terheléseknek vannak kitéve. Az ábrán az egyik oldalon befogott lapos rugó látható ( 1 és 2 ), valamint egy formázott rugó vagy formázott fémrész terhelése hajlításkor ( 3 ).

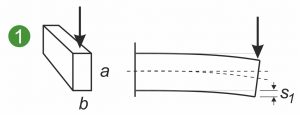
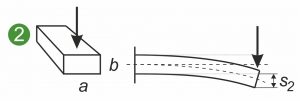
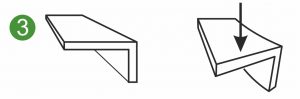
Table of Contents

A terület tengelyirányú második momentuma

Az Ia tehetetlenségi nyomaték tengelyirányú geometriai nyomatéka a laprugó keresztmetszete és a terhelés alatti laprugó görbülete közötti összefüggést írja le. A következő érvényes: minél nagyobb Ia , annál kisebb a görbület és a keresztmetszetben fellépő belső feszültségek . Ami itt lényeges, az a támadó erő irányába történő terjeszkedés. A diagram azt mutatja, hogy a függőleges erő kevésbé hajlítja meg a lapos rugót, ha azt függőlegesen rögzítik, nem pedig laposra ( 1 és 2 ). Az axiális

A terület tehetetlenségi nyomatéka a következő képletekkel számítható ki:

$Iy = \ int_ {} z ^{2} ott$

z = az y tengely függőleges távolsága a dA elemtől

$Iz = \ int_ {} y ^{2} ott$

y = a z tengely függőleges távolsága a dA elemtől

A terület biaxiális nyomatéka

Az Iyz biaxiális területi tehetetlenségi nyomatékot területi eltérési nyomatéknak vagy területi centrifugális nyomatéknak is nevezik. Az Iyz -t a terhelt alakrugók, lapos rugók és aszimmetrikus alakú fémrészek alakváltozásának és feszültségeinek kiszámítására használják ( 3 ).

$Iyz = Izy = \ int_ {} yz dA$

Ezt a mennyiséget eltérésnek vagy centrifugális nyomatéknak is nevezik. Akkor egyenlő nullával, ha az y- vagy a z-tengely a keresztmetszet szimmetriatengelye.

Iyz = 0

Származtatott mennyiségek

A területi tehetetlenségi nyomatékból számos egyéb változó is származtatható, mint például az ellenállási nyomaték és a terület tehetetlenségi sugara.

Az ellenállás pillanata

A szakasz modulusát a rugalmasság lineáris elméletében használják. Ez határozza meg a keresztmetszet szélén fellépő legnagyobb igénybevételt, a mechanikai igénybevételt. Ez a változó a terület tehetetlenségi nyomatékának és a távolságnak a hányadosa $\ alfa _m_a_x}$ a semleges szál szélétől:

$W: = \ frac{I} {\ alfa _m_a_x}$

Terület tehetetlenségi sugara

Geometriailag hasonló komponensek, például azonos szélesség-magasság arányú téglalapok esetén a körforgási terület sugara a mérethosszal is meghatározható. Ez lehetővé teszi az elhajlás és a merevség tekintetében hasonló testek összehasonlítását. A forgási terület sugara beleszámít a karcsúsági arányba.

$iy: = \ sqrt {\ frac{Iy}{A} }$

$iz: = \ sqrt {\ frac{Iz}{A} }$

$ip: = \ sqrt {\ frac{Ip}{A} }$

Itt további információkat talál a lapos rugók , alakrugók és lapos idomrugók számításáról . Ha műszaki rugót keres speciális alkalmazásához, akkor egyszerűen küldje el nekünk a kívánt rugóadatokat a kívánt darabszámmal és a rajzzal vagy a CAD adatokkal az alábbi érdeklődő gomb alatt ” Rugói megkeresés ” vagy e-mailben az info@gutekunst-formfedern.de . Rövid időn belül nem kötelező érvényű ajánlatot teszünk Önnek.

Federnanfrage

További információ: