En el diseño de resortes planos, resortes con forma y resortes con forma plana, a menudo se calcula el momento de inercia del área además del esfuerzo de flexión. El momento de inercia del área es una magnitud geométrica utilizada en la teoría de la resistencia. Se utiliza para el cálculo de deformaciones y tensiones en flexión y torsión de muelles y molduras metálicas. El momento de inercia de la zona se deriva de la sección transversal de las molduras metálicas. El momento de inercia del área se especifica en mm4. Dependiendo de la carga, se pueden distinguir dos tipos diferentes de momento de inercia de la zona.
Los siguientes gráficos muestran las secciones transversales simétricas y asimétricas de un muelle plano, un muelle con forma o un muelle con forma plana sometidos a diferentes cargas. Las ilustraciones muestran un muelle plano sujetado por un lado(1 y 2) y la carga de un muelle con forma o una moldura metálica al doblarse(3).
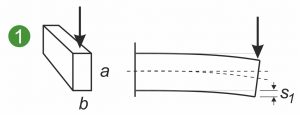
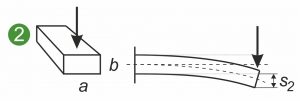
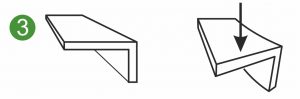
Table of Contents
Momento de inercia de la superficie axial
El momento de inercia superficial axial Ia describe la relación entre la sección transversal del muelle plano y la curvatura de un muelle plano bajo carga. Se aplica lo siguiente: cuanto mayor sea Ia, menor será la curvatura y las tensiones internas que surjan en la sección transversal. Lo esencial aquí es la expansión en la dirección de la fuerza de ataque. El diagrama ilustra que una fuerza vertical dobla menos un muelle plano cuando se sujeta de canto en lugar de plano(1 y 2). El axial
El momento de inercia del área se calcula con las siguientes fórmulas:
\Large Iy=\int_{} z^{2} dA- z = distancia perpendicular del eje y al elemento dA
- y = distancia perpendicular del eje z al elemento dA
Momento de inercia superficial biaxial
El momento de inercia superficial biaxial Iyz también se denomina momento de desviación superficial o momento centrífugo superficial. Iyz se utiliza para calcular la deformación y las tensiones en muelles con forma cargada, muelles con forma plana y piezas metálicas con forma asimétrica(3).
\Large Iyz=Izy=\int_{} yz dAEsta cantidad también se conoce como desviación o momento centrífugo. Es igual a cero si el eje y o el eje z es un eje de simetría de la sección transversal.
\Large Iyz = 0
Cantidades derivadas
A partir del momento de inercia pueden derivarse otras magnitudes, como el momento de resistencia y el radio de inercia superficial.
Par de resistencia
El módulo de sección se utiliza en la teoría de la elasticidad lineal. Esto determina la mayor tensión que se produce en el borde de la sección transversal, la tensión mecánica. Este valor es el cociente del momento de inercia del área y la distancia de la arista a la fibra neutra:
\Large W:=\frac{I}{\alpha máx}
Área de radio de inercia
Para los componentes geométricamente similares, como los rectángulos con la misma relación anchura-altura, el radio de inercia del área también puede definirse con la dimensión longitud. Esto permite comparar cuerpos que son similares en cuanto a deflexión y rigidez. El radio de inercia del área se incluye en la relación de esbeltez.
\Large iy:=\sqrt{\frac{Iy}{A}} \Large iz:=\sqrt{\frac{Iz}{A}} \Large ip:=\sqrt{\frac{Ip}{A}}
Vea aquí más información sobre el cálculo de muelles planos, muelles con forma y muelles con forma plana. Si está buscando un muelle técnico para su aplicación especial, sólo tiene que enviarnos los datos del muelle que necesita, con el número de piezas requerido y el dibujo o los datos CAD, a través del siguiente botón de consulta»Consulta sobre muelles» o por correo electrónico info@gutekunst-formfedern.de. Le haremos una oferta sin compromiso con poca antelación.
Información Adicional: