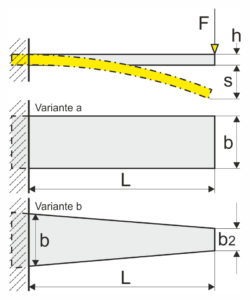
Gdy sprężyna płytkowa lub płaska jest zaciśnięta z jednej strony, maksymalne naprężenie zginające, siłę sprężyny, ugięcie sprężyny (ugięcie), grubość pióra sprężyny i współczynnik sprężystości można obliczyć w następujący sposób. Naprężenie zginające wzrasta liniowo wraz ze wzrostem siły w miejscu przyłożenia siły, gdy sprężyna płytkowa lub płaska jest zaciśnięta z jednej strony. Z prostokątną sprężyną piórową (wariant a) największe naprężenie zginające, jednak tylko w punkcie mocowania. W ten sposób prostokątna sprężyna piórowa w pełni rozwija swoje zalety tylko w punkcie mocowania. Natomiast resor trapezowy (wariant b) bardziej równomierne naprężenie zginające w przekroju. W efekcie, w zależności od rozmiaru trapezu, praca sprężynowa trapezowego resoru piórowego jest nawet trzykrotnie lepsza niż w przypadku prostokątnego resoru piórowego. Trójkątny kształt byłby idealny, ale ze względu na konstrukcję rzadko można go używać.
Table of Contents
Formuły:
Maksymalne naprężenie zginające
\Large \sigma_{{b}} = \frac{M}{W} = \frac{6 \cdot F \cdot L}{b \cdot h^{2}} \leq \sigma_{{b zul}}
Maksymalna siła sprężyny
\Large F_{{max}} = \frac{b\cdot h^{2} \cdot \sigma_{{b zul}}}{6 \cdot L}
Skok sprężyny (ugięcie)
\Large s = q_{1} \cdot \frac{L^{3}}{b \cdot h^{3}} \cdot \frac{F}{E}
\Large q_{1} dla prostokątnego resoru piórowego (wariant a) \Large q_{1} = 4
\Large q_{1} dla resoru piórowego trapezowego (wariant b) \Large q_{{1}} \approx 4 \cdot \left [ 3/ \left ( 2+b2/b \right ) \right ]
Maksymalne ugięcie sprężyny (ugięcie)
\Large s \leq q_{{2}} \cdot \frac{L^{2}}{h} \cdot \frac{\sigma_{{b zul}}}{E}
Maksymalna grubość skrzydła sprężyny
\Large h \leq q_{{2}} \cdot \frac{L^{2}}{s} \cdot \frac{\sigma_{{b zul}}}{E}
\Large q_{2} dla prostokątnego resoru piórowego (wariant a) \Large q_{2} = 2/3
\Large q_{2} dla resoru piórowego trapezowego (wariant b) \Large q_{{2}} \approx \left ( 2/3 \right ) \cdot \left [ 3/ \left ( 2+b2/b \right ) \right ]
Wiosenna stawka
\Large C = \frac{F}{s} = \frac{Ebh^{3}}{4L^{3}}
b = szerokość resoru (mm)
b2 = mniejsza szerokość trapezowej resoru piórowego (mm)
E = moduł sprężystości
F = siła sprężyny (N)
h = grubość materiału płytka sprężysta / płytka sprężyny (mm)
L = długość sprężyny płytkowej (mm)
s = skok sprężyny (mm)
Gutekunst Formfedern opracowuje i wytwarza indywidualne produkty Sprężyny płytkowe , Sprężyny płaskie i Tworzą sprężyny jako próbki, prototypy, w formacie Małe ilości i duże serie. Jeśli jesteś zainteresowany, po prostu prześlij nam poniższe Przycisk zapytania lub za pośrednictwem poczty elektronicznej info@gutekunst-formfedern.de dane żądanej sprężyny kształtowej ze szczegółami liczby sztuk i rysunkiem lub danymi CAD. W krótkim czasie przedstawimy Ci niewiążącą ofertę.
Aby uzyskać więcej informacji, zobacz: