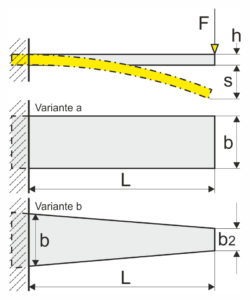
Az egyik oldalon rögzített levélrugóval vagy lapos rugóval a maximális hajlítófeszültség, rugóerő, rugóhajlás (alakváltozás), rugólap vastagság és rugósebesség a következőképpen számítható. A hajlító feszültség lineárisan növekszik az egyik oldalon rögzített levélrugóval vagy lapos rugóval, az erő növekedésével az erő kifejtésének helyén. A téglalap alakú levélrugóval (variáns a) a legnagyobb hajlítófeszültség azonban csak a befogási pontnál. Így a téglalap alakú levélrugó csak a szorítóponton fejleszti ki teljes előnyét. Ezzel szemben a trapéz alakú levélrugó (variáns b) egyenletesebb hajlítófeszültség a keresztmetszetben. Ennek eredményeként a trapéz alakú levélrugó rugós munkája a trapéz méretétől függően akár háromszor jobb, mint a téglalap alakú levélrugóé. A háromszög alakú alakzat ideális lenne, de a kialakítás miatt ritkán használható.
Table of Contents
Képletek:
Maximális hajlítófeszültség
\Large \sigma_{{b}} = \frac{M}{W} = \frac{6 \cdot F \cdot L}{b \cdot h^{2}} \leq \sigma_{{b zul}}
Maximális rugóerő
\Large F_{{max}} = \frac{b\cdot h^{2} \cdot \sigma_{{b zul}}}{6 \cdot L}
Rugós menet (elhajlás)
\Large s = q_{1} \cdot \frac{L^{3}}{b \cdot h^{3}} \cdot \frac{F}{E}
\Large q_{1} téglalap alakú laprugóhoz (a változat) \Large q_{1} = 4
\Large q_{1} trapéz alakú laprugóhoz (b változat) \Large q_{{1}} \approx 4 \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]
Maximális rugóhajlás (alakváltozás)
\Large s \leq q_{{2}} \cdot \frac{L^{2}}{h} \cdot \frac{\sigma_{b zul}}{E}
Maximális tavaszi levélvastagság
\Large h \leq q_{{2}} \cdot \frac{L^{2}}{s} \cdot \frac{\sigma_{b zul}}{E}
\Large q_{2} téglalap alakú laprugó esetén (a változat) \Large q_{2} = 2/3
\Large q_{2} trapéz alakú laprugóhoz (b változat) \Large q_{{2}} \approx \left ( 2/3 \right ) \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]
Federrate
\Large C = \frac{F}{s} = \frac{Ebh^{3}}{4L^{3}}
b = a levélrugó szélessége (mm)
b2 = a trapéz alakú levélrugó kisebb szélessége (mm)
E = rugalmassági modulus
F = rugóerő (N)
h = anyagvastagság rugólemez / rugólevél (mm)
L = levélrugó hossza (mm)
s = rugós menet (mm)
A Gutekunst Formfedern egyedi termékeket fejleszt és gyárt Levélrugók , Lapos rugók és Forma rugók minták, prototípusok, in Kis mennyiségben és nagy sorozatok. Ha érdekli, egyszerűen küldje el nekünk az alábbiakat Érdeklődés gomb vagy e-mailben info@gutekunst-formfedern.de a kívánt alakú rugó adatai a darabszám és a rajz részleteivel, vagy a CAD adatok. Rövid időn belül nem kötelező érvényű ajánlatot teszünk Önnek.
További információ: