Výpočet listové pružiny › Gutekunst Formfedern GmbH › berechnen, Biegespannung, Blattfeder, Blattfeder Berechnung, Federblattstärke, Federrate, Flachfeder, Formeln, Síla pružiny

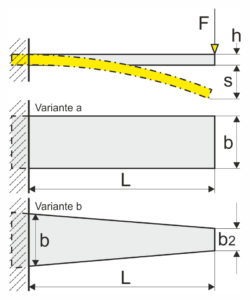
Když je listová pružina nebo plochá pružina upnuta na jedné straně, lze maximální napětí v ohybu, sílu pružiny, průhyb pružiny (průhyb), tloušťku listu pružiny a rychlost pružiny vypočítat následovně. Napětí v ohybu se lineárně zvyšuje s listovou pružinou nebo plochou pružinou upnutou na jedné straně se zvýšením síly v místě působení síly. S obdélníkovou listovou pružinou (varianta a) nejvyšší napětí v ohybu, ale pouze v místě upnutí. Obdélníková listová pružina tedy plně využívá své výhody pouze v místě sevření. Naproti tomu lichoběžníková listová pružina (varianta b) rovnoměrnější ohybové napětí v průřezu. Výsledkem je, že pružinová práce lichoběžníkové listové pružiny je až třikrát lepší než u obdélníkové listové pružiny, v závislosti na velikosti lichoběžníku. Ideální by byl trojúhelníkový tvar, ale vzhledem k designu jej lze použít jen zřídka.

Table of Contents

Vzorce:

Maximální napětí v ohybu

$\Large \sigma_{{b}} = \frac{M}{W} = \frac{6 \cdot F \cdot L}{b \cdot h^{2}} \leq \sigma_{{b zul}}$

Maximální síla pružiny

$\Large F_{{max}} = \frac{b\cdot h^{2} \cdot \sigma_{{b zul}}}{6 \cdot L}$

Pojezd pružiny (průhyb)

$\Large s = q_{1} \cdot \frac{L^{3}}{b \cdot h^{3}} \cdot \frac{F}{E}$

$\Large q_{1}$ pro obdélníkovou listovou pružinu (varianta a) $\Large q_{1}$ = 4

$\Large q_{1}$ pro lichoběžníkovou listovou pružinu (varianta b) $\Large q_{{1}} \approx 4 \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]$

Maximální průhyb pružiny (průhyb)

$\Large s \leq q_{{2}} \cdot \frac{L^{2}}{h} \cdot \frac{\sigma_{{b zul}}}{E}$

Maximální tloušťka listu pružiny

$\Large h \leq q_{{2}} \cdot \frac{L^{2}}{s} \cdot \frac{\sigma_{{b zul}}}{E}$

$\Large q_{2}$ pro obdélníkovou listovou pružinu (varianta a) $\Large q_{2}$ = 2/3

$\Large q_{2}$ pro lichoběžníkovou listovou pružinu (varianta b) $\Large q_{{2}} \approx \left ( 2/3 \right ) \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]$

Federrate

$\Large C = \frac{F}{s} = \frac{Ebh^{3}}{4L^{3}}$

b = šířka listové pružiny (mm)

b2 = menší šířka lichoběžníkové listové pružiny (mm)

E = modul pružnosti

F = síla pružiny (N)

h = tloušťka materiálu pružinová deska / list pružiny (mm)

L = délka listové pružiny (mm)

s = zdvih pružiny (mm)

Gutekunst Formfedern vyvíjí a vyrábí jednotlivé produkty Listové pružiny , Ploché pružiny a Tvarové pružiny jako vzorky, prototypy, v Malá množství a velké série. Pokud máte zájem, jednoduše nám zašlete pod následující Tlačítko poptávky nebo prostřednictvím e-mailu info@gutekunst-formfedern.de data požadované tvarované pružiny s podrobnostmi o počtu kusů a výkresu nebo CAD data. V krátké době vám dáme nezávaznou nabídku.

Poptávka

Další informace viz: