Leaf spring calculation › Gutekunst Formfedern GmbH

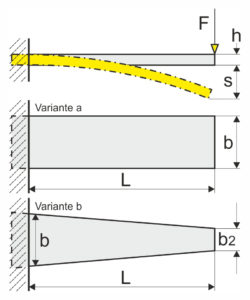
With the leaf spring or flat spring clamped on one side, the maximum bending stress, spring force, spring deflection (deflection), spring leaf thickness and spring rate can be calculated as follows. The bending stress increases linearly with the leaf spring or flat spring clamped on one side with an increase in force at the point of force application. With the rectangular leaf spring (variant a) the highest bending stress only at the clamping point. Thus, the rectangular leaf spring only develops its full benefit at the clamping point. In contrast, the trapezoidal leaf spring (variant b) a more uniform bending stress in cross section. As a result, the spring work of the trapezoidal leaf spring is up to three times better than that of the rectangular leaf spring, depending on the size of the trapezoid. A triangular shape would be ideal, but due to the design it can rarely be used.

Table of Contents

Formulas:

Maximum bending stress

$\sigma_{<wpml_curved wpml_value='b'></wpml_curved>} = \frac<wpml_curved wpml_value='M'></wpml_curved><wpml_curved wpml_value='W'></wpml_curved> = \frac{6 \cdot F \cdot L}{b \cdot h^<wpml_curved wpml_value='2'></wpml_curved>} \leq \sigma_{{b zul}}$

Maximum spring force

$F_{<wpml_curved wpml_value='max'></wpml_curved>} = \frac{b\cdot h^<wpml_curved wpml_value='2'></wpml_curved> \cdot \sigma_{{b zul}}}{6 \cdot L}$

Spring travel (deflection)

$s = q_<wpml_curved wpml_value='1'></wpml_curved> \cdot \frac{L^<wpml_curved wpml_value='3'></wpml_curved>}{b \cdot h^<wpml_curved wpml_value='3'></wpml_curved>} \cdot \frac<wpml_curved wpml_value='F'></wpml_curved><wpml_curved wpml_value='E'></wpml_curved>$

$q_<wpml_curved wpml_value='1'></wpml_curved>$ for rectangular leaf spring (variant a) $q_<wpml_curved wpml_value='1'></wpml_curved>$ = 4

$q_<wpml_curved wpml_value='1'></wpml_curved>$ for trapezoidal leaf spring (variant b) $q_{<wpml_curved wpml_value='1'></wpml_curved>} \approx 4 \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]$

Maximum spring deflection (deflection)

$s \leq q_{<wpml_curved wpml_value='2'></wpml_curved>} \cdot \frac{L^<wpml_curved wpml_value='2'></wpml_curved>}<wpml_curved wpml_value='h'></wpml_curved> \cdot \frac{\sigma_{{b zul}}}<wpml_curved wpml_value='E'></wpml_curved>$

Maximum spring leaf thickness

$h \leq q_{<wpml_curved wpml_value='2'></wpml_curved>} \cdot \frac{L^<wpml_curved wpml_value='2'></wpml_curved>}<wpml_curved wpml_value='s'></wpml_curved> \cdot \frac{\sigma_{{b zul}}}<wpml_curved wpml_value='E'></wpml_curved>$

$q_<wpml_curved wpml_value='2'></wpml_curved>$ for rectangular leaf spring (variant a) $q_<wpml_curved wpml_value='2'></wpml_curved>$ = 2/3

$q_<wpml_curved wpml_value='2'></wpml_curved>$ for trapezoidal leaf spring (variant b) $q_{<wpml_curved wpml_value='2'></wpml_curved>} \approx \left ( 2/3 \right ) \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]$

Spring rate

$C = \frac<wpml_curved wpml_value='F'></wpml_curved><wpml_curved wpml_value='s'></wpml_curved> = \frac{Ebh^<wpml_curved wpml_value='3'></wpml_curved>}{4L^<wpml_curved wpml_value='3'></wpml_curved>}$

b = width of leaf spring (mm)

b2 = smaller width of trapezoidal leaf spring (mm)

E = modulus of elasticity

F = spring force (N)

h = material thickness spring plate / spring leaf (mm)

L = length of leaf spring (mm)

s = spring travel (mm)

Would you like to find out more about the calculation of leaf springs and flat springs or which spring is best suited for your special application? Then contact our technical department by phone at (+49) 07445 8516-0 or info@gutekunst-formfedern.de .

Gutekunst Formfedern develops and manufactures individual products Leaf springs , Flat springs and Form springs as samples, prototypes, in Small quantities and large series. If you are interested, simply send us under the following Inquiry button the data of the desired shaped spring with details of the number of pieces and the drawing or the CAD data We will prepare a non-binding offer for you at short notice.

Anfrage Formfedern & Blattfedern

For more information, see: