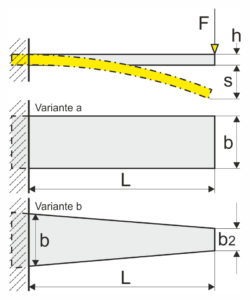
Avec le ressort à lame ou le ressort plat serré d’un côté, la contrainte de flexion maximale, la force du ressort, la flèche du ressort (flèche), l’épaisseur de la lame du ressort et la raideur du ressort peuvent être calculés comme suit. La contrainte de flexion augmente linéairement avec le ressort à lame ou le ressort plat serré d’un côté avec une augmentation de la force au point d’application de la force. Avec le ressort à lame rectangulaire (variante a) la contrainte de flexion la plus élevée uniquement au point de serrage. Ainsi, le ressort à lame rectangulaire ne développe pleinement son avantage qu’au point de serrage. En revanche, le ressort à lame trapézoïdale (variante b) une contrainte de flexion plus uniforme en section transversale. En conséquence, le travail du ressort du ressort à lame trapézoïdale est jusqu’à trois fois meilleur que celui du ressort à lame rectangulaire, en fonction de la taille du trapèze. Une forme triangulaire serait idéale, mais en raison de sa conception, elle peut rarement être utilisée.
Table of Contents
Formules:
Contrainte de flexion maximale
\Large \sigma_{{b}} = \frac{M}{W} = \frac{6 \cdot F \cdot L}{b \cdot h^{2}} \leq \sigma_{{b zul}}
Force maximale du ressort
\Large F_{{max}} = \frac{b\cdot h^{2} \cdot \sigma_{{b zul}}}{6 \cdot L}
Course du ressort (déflexion)
\Large s = q_{1} \cdot \frac{L^{3}}{b \cdot h^{3}} \cdot \frac{F}{E}
\Large q_{1} pour ressort à lame rectangulaire (variante a) \Large q_{1} = 4
\Large q_{1} pour le ressort à lames trapézoïdal (variante b) \Large q_{{1}} \approx 4 \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]
Déformation maximale du ressort (déflexion)
\Large s \leq q_{{2}} \cdot \frac{L^{2}}{h} \cdot \frac{\sigma_{{b zul}}}{E}
Épaisseur maximale des lames de ressort
\Large h \leq q_{{2}} \cdot \frac{L^{2}}{s} \cdot \frac{\sigma_{{b zul}}}{E}
\Large q_{2} pour ressort à lame rectangulaire (variante a) \Large q_{2} = 2/3
\Large q_{2} pour le ressort à lames trapézoïdal (variante b) \Large q_{{2}} \approx \left ( 2/3 \right ) \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]
Federrate
\Large C = \frac{F}{s} = \frac{Ebh^{3}}{4L^{3}}
b = largeur du ressort à lame (mm)
b2 = largeur plus petite du ressort à lame trapézoïdale (mm)
E = module d’élasticité
F = force du ressort (N)
h = épaisseur du matériau plaque de ressort / lame de ressort (mm)
L = longueur du ressort à lame (mm)
s = course du ressort (mm)
Gutekunst Formfedern développe et fabrique des produits individuels Ressorts à lames , Ressorts plats et Ressorts de forme comme échantillons, prototypes, en Petites quantités et grandes séries. Si vous êtes intéressé, envoyez-nous simplement sous ce qui suit Bouton d’enquête ou par e-mail info@gutekunst-formfedern.de les données du ressort façonné souhaité avec des détails sur le nombre de pièces et le dessin ou les données CAO. Nous vous ferons une offre sans engagement dans un bref délai.
Pour plus d’informations, consultez: