 The tension energy is generated due to the elastic deformation of a metal spring. It is a form of potential energy and indicates how much mechanical work occurs when the metal spring is loaded or tensioned. To do mechanical work, will mechanical energy needed. This can be found everywhere in our everyday lives: An internal combustion engine converts the chemical energy in fuel into mechanical kinetic energy through combustion, an electric motor generates mechanical energy from electrical energy, and a metal spring stores mechanical energy in the form of tension energy when it is loaded. Besides the tension energy, one can discover other types of mechanical energy:
The tension energy is generated due to the elastic deformation of a metal spring. It is a form of potential energy and indicates how much mechanical work occurs when the metal spring is loaded or tensioned. To do mechanical work, will mechanical energy needed. This can be found everywhere in our everyday lives: An internal combustion engine converts the chemical energy in fuel into mechanical kinetic energy through combustion, an electric motor generates mechanical energy from electrical energy, and a metal spring stores mechanical energy in the form of tension energy when it is loaded. Besides the tension energy, one can discover other types of mechanical energy:
- Every body has one due to its mass in the earth’s gravitational field potential energy (Position or altitude energy). For example, it causes free fall.
- When a body moves over a surface, the frictional resistance generates heat, and thus heat Frictional energy .
- The faster a body is moved, the higher it is kinetic energy , also Kinetic energy called.
- If the body performs a circular motion, it lies Rotational energy in front.
Table of Contents
Conversion of mechanical energy in metal springs
In a burdened Metal spring is mechanical energy in the form of tension energy. This tension energy is released when the load is released. For example, if a ball is in front of the metal spring, it sets it in motion. The tension energy of the metal spring can be used to accelerate other bodies. As soon as the acceleration work has been done, the ball has kinetic energy. After this Energy Conservation Act the energy is not lost in the process, it is only converted. This conversion of mechanical forms of energy is the basis of all processes in mechanics. However, in a non-perfect system (natural environment), this kinetic energy of the ball is lost during the movement due to frictional forces and air resistance down to zero.
Calculation of the clamping energy
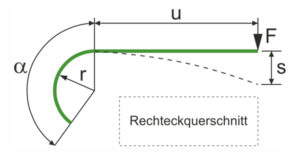 The tension energy is stored in a metal spring when tensioned. It depends on the loaded spring travel s (mm) of the metal spring and the spring constant R. (N / mm).
The tension energy is stored in a metal spring when tensioned. It depends on the loaded spring travel s (mm) of the metal spring and the spring constant R. (N / mm).
The following applies to metal springs:
- The spring constant R (N/mm) indicates the hardness of the metal spring
- The clamping energy ESpann is proportional to the spring constant R (N/mm): ESpann ~ R
- The clamping energy EStension is proportional to the square of the spring travel s (mm): ESpann ~ s²
Formula for span energy:
ESpann=12 · R · s2
To the spring constant R. (N / mm) for Flat and shaped springs in a load test (for the acting force F. is the spring deflection s measured), the following formula applies:
R=F2 – F1 · s2 – s1
F1 = Spring force preloaded
s1 = Spring deflection preloaded
F2 = Spring force loaded
s2 = Loaded spring deflection
See more information about the Calculation of shaped springs , Flat springs , Contact springs and Leaf springs . The technical experts at Gutekunst Formfedern support you in designing the right metal spring. Simply send “ Spring request ” or via email info@gutekunst-formfedern.de the data of your desired metal spring with details of the number of pieces and the drawing or the CAD data. We will prepare a non-binding offer for you at short notice.
For more information:
