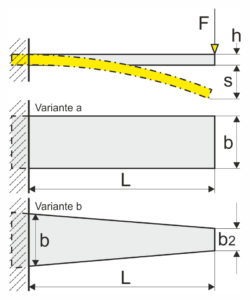
Con la molla a balestra o la molla piatta bloccata su un lato, la sollecitazione di flessione massima, la forza della molla, la flessione della molla (flessione), lo spessore della foglia della molla e la rigidità della molla possono essere calcolate come segue. La sollecitazione di flessione aumenta linearmente con la molla a balestra o la molla piatta bloccata su un lato con un aumento della forza nel punto di applicazione della forza. Con la balestra rettangolare (variante a) la massima sollecitazione di flessione solo nel punto di serraggio. Pertanto, la molla a balestra rettangolare dispiega il suo pieno vantaggio solo nel punto di bloccaggio. Al contrario, la balestra trapezoidale (variante b) uno sforzo di flessione più uniforme nella sezione trasversale. Di conseguenza, il lavoro della molla della molla a balestra trapezoidale è fino a tre volte migliore di quello della molla a balestra rettangolare, a seconda delle dimensioni del trapezio. Una forma triangolare sarebbe l’ideale, ma a causa del design può essere utilizzata raramente.
Table of Contents
Formule:
Massimo sforzo di flessione
\Large \sigma_{{b}} = \frac{M}{W} = \frac{6 \cdot F \cdot L}{b \cdot h^{2}} \leq \sigma_{{b zul}}
Forza massima della molla
\Large F_{{max}} = \frac{b\cdot h^{2} \cdot \sigma_{b zul}}{6 \cdot L}
Corsa della molla (deflessione)
\Large s = q_{1} \cdot \frac{L^{3}}{b \cdot h^{3}} \cdot \frac{F}{E}
\Large q_{1} per molla a balestra rettangolare (variante a) \Large q_{1} = 4
\Large q_{1} per molla a balestra trapezoidale (variante b) \Large q_{{1}} \approx 4 \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]
Flessione massima della molla (flessione)
\Large s \leq q_{{2}} \cdot \frac{L^{2}}{h} \cdot \frac{sigma_{b zul}}{E}
Spessore massimo della foglia primaverile
\Large h \leq q_{{2}} \cdot \frac{L^{2}}{s} \cdot \frac{\sigma_{b zul}}{E}
\Large q_{2} per molla a balestra rettangolare (variante a) \Large q_{2} = 2/3
\Large q_{2} per molla a balestra trapezoidale (variante b) \Large q_{{2}} \approx \left ( 2/3 \right ) \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]
Federrate
]\Large C = \frac{F}{s} = \frac{Ebh^{3}}{4L^{3}}
b = larghezza della balestra (mm)
b2 = minore larghezza della balestra trapezoidale (mm)
E = modulo di elasticità
F = forza della molla (N)
h = spessore materiale piastra della molla / balestra (mm)
L = lunghezza della balestra (mm)
s = corsa della molla (mm)
Gutekunst Formfedern sviluppa e produce singoli prodotti Molle a balestra , Molle piatte e Forma molle come campioni, prototipi, in Piccole quantità e grandi serie. Se sei interessato, inviaci semplicemente sotto Pulsante di richiesta o tramite e-mail info@gutekunst-formfedern.de i dati della molla sagomata desiderata con il dettaglio del numero di pezzi e il disegno o il dato CAD. Ti faremo un’offerta non vincolante con breve preavviso.
Per ulteriori informazioni, vedere: