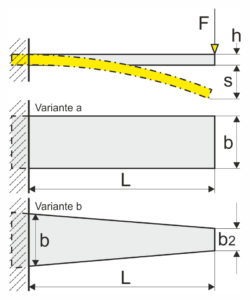
Con el resorte plano o el resorte plano sujeto en un lado, la tensión máxima de flexión, la fuerza del resorte, la deflexión del resorte (deflexión), el espesor de la hoja del resorte y la tasa de resorte se pueden calcular de la siguiente manera. La tensión de flexión aumenta linealmente con la ballesta o el resorte plano sujeto en un lado con un aumento de la fuerza en el punto de aplicación de la fuerza. Con la ballesta rectangular (variante a) el esfuerzo de flexión más alto, sin embargo, solo en el punto de sujeción. Por lo tanto, la ballesta rectangular solo desarrolla todo su beneficio en el punto de sujeción. Por el contrario, la ballesta trapezoidal (variante b) un esfuerzo de flexión más uniforme en la sección transversal. Como resultado, el trabajo elástico de la ballesta trapezoidal es hasta tres veces mejor que el de la ballesta rectangular, dependiendo del tamaño del trapezoide. Una forma triangular sería ideal, pero debido al diseño, rara vez se puede usar.
Table of Contents
Fórmulas:
Esfuerzo de flexión máximo
\Large \sigma_{{b}} = \frac{M}{W} = \frac{6 \cdot F \cdot L}{b \cdot h^{2}} \leq \sigma_{{b zul}}
Fuerza de resorte máxima
\Large F_{{max}} = \frac{b\cdot h^{2} \cdot \sigma_{b zul}} {6 \cdot L}
Viaje de resorte (deflexión)
\Large s = q_{1} \cdot \frac{L^{3}}{b \cdot h^{3}} \cdot \frac{F}{E}
\Large q_{1} para ballesta rectangular (variante a) \Large q_{1} = 4
\Large q_{1} para ballesta trapezoidal (variante b) \Large q_{1} \approx 4 \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]
Deflexión máxima del resorte (deflexión)
\Large s \leq q_{{2}} \cdot \frac {L^{2}}{h} \cdot \frac {\sigma_{b zul}}{E}
Espesor máximo de la hoja de resorte
\Large h \leq q_{{2}} \cdot \frac{L^{2}}{s} \cdot \frac{\sigma_{{b zul}}}{E}
\Large q_{2} para ballesta rectangular (variante a) \Large q_{2} = 2/3
\Large q_{2} para ballesta trapezoidal (variante b) \Large q_{2} \approx \left ( 2/3 \right ) \cdot \left [ 3/ \left ( 2+b2/b \right )\right ]
Tasa de resorte
\Large C = \frac{F}{s} = \frac{Ebh^{3}}{4L^{3}}
b = ancho de la ballesta (mm)
b2 = menor ancho de la ballesta trapezoidal (mm)
E = módulo de elasticidad
F = fuerza del resorte (N)
h = espesor del material placa de resorte / hoja de resorte (mm)
L = longitud de la ballesta (mm)
s = recorrido del resorte (mm)
Gutekunst Formfedern desarrolla y fabrica productos individuales Hojas primaverales , Resortes planos y Muelles de forma como muestras, prototipos, en Pequeñas cantidades y grandes series. Si está interesado, simplemente envíenos bajo la siguiente Botón de consulta o por correo electrónico info@gutekunst-formfedern.de los datos del resorte de forma deseada con detalles del número de piezas y el dibujo o los datos CAD. Le haremos una oferta sin compromiso con poca antelación.
Para más información, ver: