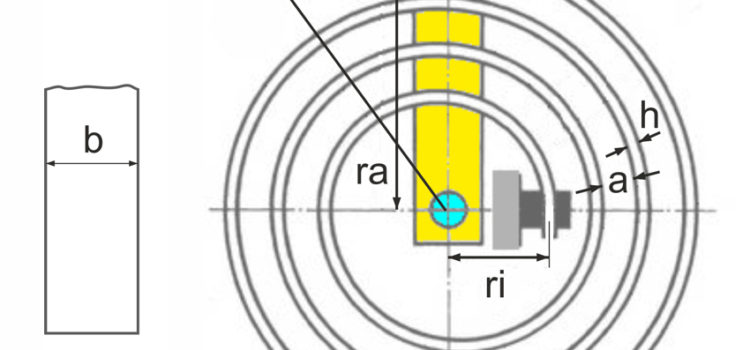
L’utilisation des ressorts métalliques est très variée. En fonction de la fonction de base (courbe de force, mouvement, montage), il existe un choix de ressort privilégié. Qu’il s’agisse de ressorts métalliques plats ou en fil métallique, découvrez ici ce qui
Forme des ressorts, des ressorts plats et des ressorts à lames
Les ressorts de forme, les ressorts plats et les ressorts à lames comptent parmi les plus anciens types de ressorts métalliques et se sont imposés comme des éléments de construction indispensables dans de nombreux secteurs industriels. Ils font aujourd’hui
Offre ressorts plats
Les ressorts plats sont fabriqués individuellement selon les dessins, les données CAO, les données dimensionnelles ou les exigences du client Acier de bande de ressort comme Feuilles d’acier à ressort poinçonné , laser ou gravé. Les ressorts plats peuvent être
Calculer les ressorts hélicoïdaux
Ressorts hélicoïdaux sera éteint Acier de bande de ressort produit. Les ressorts en spirale sont enroulés dans un plan de la spirale d’Archimède. La distance constante entre les spires (a) empêche les spires individuelles de se toucher et garantit que
Sélection de ressorts à lames
Sous le terme générique ressorts à lames devenir différent Types de plumes résumé, qui peut être utilisé dans d’innombrables applications. Leur choix s’étend des simples ressorts en spirale et des ressorts plats aux ressorts de forme complexes et aux ressorts
Aperçu des types de ressorts
Qu’entend-on par ressorts? Les ressorts sont des composants techniques en acier à ressort qui peuvent se déformer élastiquement. Lorsqu’ils sont soumis à des contraintes, ils cèdent et absorbent la force. Lorsqu’ils se détendent, ils libèrent cette énergie et reviennent à
Ressorts hélicoïdaux sur mesure
Que sont les ressorts hélicoïdaux? Les ressorts hélicoïdaux sont constitués de ressorts hélicoïdaux Acier de bande de ressort ou matériau plat et sont fabriqués individuellement selon les exigences du client. Ils sont enroulés dans un plan suivant la spirale d’Archimède.